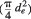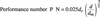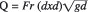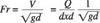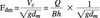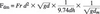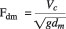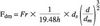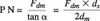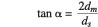Designing stilling basins
19 June 2007Arun Goel presents hydraulic model studies of stilling basins for square shaped outlets
As water flows over the spillway or through a tunnel or pipe outlet into the downstream channel, it has a very high kinetic energy. The excess energy has to be dissipated so that it does not endanger the stability of bed and banks of the downstream channel. This dissipation of energy is achieved by an energy dissipator known as the stilling basin. In the case of pipe outlets, water issues in the form of high velocity three-dimensional concentrated jet, which needs to be spread into the full width of the basin before significant energy dissipation takes place. This spreading of the jet requires an additional length of the basin compared to spillways / weirs.
A number of stilling basin models have been recommended for pipe outlets, such as USBR impact type VI (Bradely & Peterka 1957), Manifold type (Fiala & Albertson 1961), Contra costa energy dissipator (Keim 1962), USU energy dissipator (Flammer et al. 1970), Counter current type energy dissipator (Vollmer & Khader 1971), Garde energy dissipator (Garde & Saraf 1986), Smith's (1988), Goel & Verma (1999, 2000, 2001, 2006) and Verma & Goel (2000, 2003) etc. A brief literature review revealed that there is no direct design of energy disspator for the pipe outlet having square shape. Thus efforts are made in this paper to suggest new designs of energy dissipaters for square shape outlets for inflow Froude number Fr = 6.83. The initial design of the basin was based on the design as recommended by USBR impact type VI stilling basin for square shaped pipe equivalent of circular shape. The study is aimed at suggesting new designs of basins of shorter length and having higher efficiency as compared to the equivalent USBR impact type VI stilling basin for inflow Froude number Fr = 6.83. The dimensions of models are worked out on the basis of US Bureau of Reclamation (Lancastre 1987). In the present study, new shapes of splitter blocks like square, triangular and wedge shaped along with a rectangular, sloping and rounded end sills were tested for proper spreading of the jet so as to improve the performance of the new designs as compared to equivalent USBR type VI stilling basin model for the square shape outlets.
Design calculations of energy dissipator model
The dimensions of USBR impact type VI stilling basin model (Lancastre 1987) for a square shape outlet of 4cm size were calculated for an inflow Froude number Fr = 6.83. If the shape of the outlet opening is other than circular, than the area of opening is converted into equivalent diameter as mentioned by Bradley & Peterka (1957) and Froude number is calculated on the basis of equivalent diameter de in place of diameter d. Since the shape of the pipe outlet chosen was square, then as per USBR impact type VI stilling basin, the equivalent diameter of the circular pipe is calculated as below:
Area of square opening (d x d) = area of equivalent circular opening

Substituting d (dimension of square pipe ) = 4cm in above relation, we get equivalent diameter de = 4.51cm. The width of stilling basin model is expressed as:
W / de = 3 Fr0.55
For the given values of Fr = 6.83, de = 4.51cm
By using above relation, we can calculate the following parameters for the stilling basin:
* Width of stilling basin W = 38.96cm = 9.74d
* Length of basin L = 1.33W = 51.82cm = 12.95d
* Height of end sill = 0.17W = 6.63cm = 1.66d
* Hood of impact wall = 0.17W = 6.63cm = 1.66d
* Height of impact wall = 0.37W = 14.43cm = 3.61d
* Location of impact wall from exit of the outlet = 0.5W = 19.5cm = 4.87d
* Position of floor of basin below the invert level of the outlet = 0.17W = 6.63cm = 1.66d
* Tail water depth = 0.17W+ 0.37W/2 = 0.36W = 13.83cm = 3.46d
Wedge shaped blocks
Rectangular baffle blocks are provided inside the stilling basins because the rectangular shape offers maximum drag. However, theoretical analysis does not take into consideration the non-uniform, turbulent and three-dimensional flow conditions around the blocks in a stilling basin. The problem of reattachment of flow on the sides of rectangular block reduces the wake area and thereby, the drag. On the basis of experimental studies, Pillai (1963,1964,1966,1969) had shown that the wedge shaped baffle block of vertex angle 120° cut back at 90° on the downstream side offers more drag due to increase in the wake area. A strong circulatory movement of water with vertical axis was formed on either side of the block in the cutback portion resulting in the increased wake area. The chances of cavitation on such blocks are also minimised, because the downstream portion of the block is shaped in such a way that the boundaries of blocks are away from the regions where the cavities collapse (Pillai & Jayaraman 1967).
The wedge shaped baffle blocks of vertex angle 150° and cut back on sides at 90° were adopted for the development of the stilling basin for spillways and barrages with low inflow Froude numbers Fr = 2.5 to 4.5 (Pillai & Goel 1989, 1994). Such types of blocks were used for development of stilling basin models (Verma & Goel 2000, 2003) and (Goel & Verma 1999, 2001,2006). In the present study, a similar wedge shaped block is considered.
Experiment set up
The experiments were conducted in the Fluid Mechanics Laboratory of the National Institute of Technology. A 12m long, 0.60m wide and 0.90m deep flume was used to conduct the experiments. One 15 HP centrifugal pump was installed in the supply pipe for recirculation of flow. At the end of the flume, a tailgate was provided for regulating the tail water depth. The model pipe outlet having internal size d = 4cm was centrally located within the flume with its downstream face flushed with vertical masonry wall. A wooden floor on the bed of stilling basin was provided to facilitate the fixing of appurtenances required for different geometries of the stilling basin models. An erodible bed consisting of sand material passing through 2.36mm size Indian Standard sieve and retained on 1.18mm size Indian Standard sieve was filled on the downstream of the stilling basin. The run time for each model was kept as one hour. A depth of flow equal to 3.46d as recommended by Bradley & Peterka (1957) corresponding to Fr = 6.83, was maintained.
Experimental procedure
The model of the required geometry of the stilling basin was fabricated in the flume. The granular material for the erodible bed was filled and leveled up to the top of the end sill. The pump was switched on and initially a very low flow was allowed through the pipe outlet into the flume and the required tail water depth was obtained by adjusting the tailgate. The flow to the flume was gradually raised according to the desired outlet Froude number. At the end of the experiment, the pump was stopped and the tailgate was closed and the water inside the flume was drained out slowly without causing any disturbance to the developed scour pattern on the erodible bed. The scour parameters such as magnitude of maximum depth of scour (dm) and its distance from the end sill (ds) were measured using a pointer gauge and scale (Goel & Verma 2006). All the tests on all the stilling basin models were conducted for the same run time in a similar manner.
Performance criteria
The performance of a stilling basin is a function of outlet inflow Froude number (Fr), size of square pipe outlet (d), normal tail water depth of flow (h), maximum depth of scour (dm) and its location after the end sill (ds). A stilling basin model resulting into smaller depth of scour at a larger distance is considered to have better performance as compared to another stilling basin which results in larger depth of scour at a smaller distance, when tested under similar conditions.
The scour Froude number Fdm based on mean velocity of flow in the channel Vc and depth of maximum scour dm can be expressed as

If the scour pattern is assumed to be parabolic, the value of tan ± is the slope of the tangent drawn to the base parabola of the depth of maximum scour downstream of the end sill.

These two parameters are combined into one non-dimensional number Performance number and termed as P N

The inflow Froude number of the square pipe outlet in terms of outlet discharge Q can be expressed as


The scour Froude number can be written as

Where B is the width of stilling basin. In the present case B = 9.74d.
From equations (5) and (6)


Substituting this value of Fdm in the equation (4) and Fr = 6.83, h = 13.83cm as per USBR type VI basin

A higher value of performance number indicates a better performance of a stilling basin model.
Experimental scheme
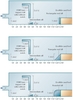
The equivalent stilling basin model of USBR impact type VI, for a square pipe outlet size d = 4cm was designed and fabricated for Fr = 6.83. This model named as SQA-1 has an impact wall with notch placed at 4.87d from the exit of the outlet with a gap at the bottom equal to 1.66d and a rectangular end sill of height 1.66d (Figure 1). The USBR stilling basin model SQA-2 (Figure 2) with an impact wall with notch and a sloping end sill (1V: 1H) of height 1.66d was designed. A new stilling basin model namely SQA-3 similar to SQA-1 was also fabricated in which the rectangular end sill was replaced by a rounded end sill of height 1.66d (Figure 3). This model named as SQA-4 has an impact wall without notch placed at 4.87d from exit of the outlet with a bottom gap 1.66d and a rectangular end sill of height 1.66d (Figure 1). The USBR stilling basin model SQA-5 (Figure 2) with an impact wall without notch and a sloping end sill (1V: 1H) of height 1.66d was designed. A new stilling basin model namely SQA-6 similar to SQA-4 was also fabricated in which the rectangular end sill was replaced by a rounded end sill of height 1.66d (Figure 3). Three stilling basin models named as SQA-7, SQA-8 and SQA-9 (Figure 4, 5, 6) were tested by adding an intermediate sill (Sloping 1V: 2H) of height 0.5d below the impact wall in the models SQA-4 to SQA-6 in length of basin 12.9d. Further new models named SQA-10 to SQA-15 were tested by introducing a splitter block of different shapes and sizes (Figure 7a, b, c, d, e, f) in order to improve the performance in the length of the basin equal to 10.9d. Further new models namely SQA-16 to SQA-21 were tested by introducing a splitter block of different shapes and sizes (Figure 7a,b, c, d, e, f) in order to study the performance in the length of the basin equal to 10.9d but with a sloping end sill (1V:1H) instead of a rounded end sill of the same height. The detail of models tested is described in the Table 1.
Results
The experimental data collected in the present study has been analyzed in the following paragraphs for different lengths of stilling basin models keeping in view the performance of best base model SQA-5. The calculated values of performance numbers (PN) for various stilling basin models are given in Table 2.
Models with basin length = 12.9d
The values of Performance number of basic models of USBR impact type VI basin namely SQA-1 (PN = 0.15) and SQA-2 (PN = 0.22) indicate that the USBR model SQA-2 (PN = 0.22) with a sloping end sill and impact wall with notch, has a better performance in comparison to USBR model SQA-1. The stilling basin models SQA-3 (PN = 0.44) with a rounded end sill has the highest PN as compared to models SQA-1 and SQA-2. The notches allowed the high velocity jet to go unobstructed and caused more scour. When impact wall without notches was used in models SQA-4(PN = 0.20), SQA-5(PN = 0.29) and SQA-6(PN = 0.56), the values of performance number improved in general but the model SQA-6(PN = 0.56) performed the best as indicated by the highest PN value mentioned in Table 2.
Introduction of intermediate sill in the models SQA-7, SQA-8 and SQA-9 increased the PN values of all the models to 0.25, 0.56, 0.87 respectively. It can also be noted that the model SQA-9 (PN = 0.87) with rounded end sill performs better as compared to models with rectangular and sloping end sill and is best in this series of models.
Models with basin length = 10.9d
In the next series, a splitter block of different shapes & width like square 0.6d width, square 1d width, triangle 1d width, triangle 1.4d width, triangle 2d width and wedge shaped 1d width as shown in Figure 7 a, b, c, d, e, & f are placed at 1d distance from the exit of the outlet in the models SQA-10 to SQA-15 respectively. Similar splitter blocks were provided in models SQA-16 to SQA-21 also. But in the models SQA-11 to SQA-15 (Figure 9) a rounded end sill is used whereas in the models SQA-16 to SQA-21 a sloping end sill is provided Figure 8). The models SQA-10 to model SQA-15 showed the PN as 0.44, 0.42, 0.59, 0.41, 0.31 and 0.71 respectively as shown in the Table 2. The values of PN improved in all the models. Similarly the models SQA-16 to model SQA-21 showed the PN as 0.30, 0.30, 0.36, 0.20, 0.21 and 0.51 respectively as shown in Table 2. The models with rounded end sill (SQA-10 to model SQA-15) are performing better than models of sloping end sill (SQA-16 to model SQA-21) with other arrangements remaining the same. But the model SQA-15 as shown in Figure 8, with a wedge shaped block of width 1d placed at a distance of id form exit of the outlet, a USBR impact type wall with a gap at bottom equal to 1.66d, an intermediate sill of height 0.5d (slope1V: 2H) at 5d and a rounded end sill of height 1.66 at the end is performing the best in all the models tested.
Further some of the selected models were tested for effect on performance on tailwater depth and running time of longer duration and performance were studied as discussed below.
Effect of tailwater on performance
The basic USBR model SQA-5, SQA-6 in 12.9d length and the model SQA-15, SQA-21 in 10.9d length were run independent of tailwater (0.59 times the used tailwater) for one hour to study the effect of tailwater on the performance. The observed values of maximum depth of scour are given in Table 3. The values of PN are 0.15, 0.18 for models SQA-5, SQA-6 and 0.17, 0.12 for models SQA-15, SQA-21. The perusal of results shows that the value of PN in the model SQA-15 is more than the USBR model SQA-5 of larger length of the basin. This means that the newly proposed model is still performing better when tested without tailwater depth.
Effect of running time on performance
The basic USBR model SQA-5, SQA-6 and the best performing model SQA-15, SQA-21 were run continuously for 8 hours with the given constant tailwater to check the effect of running time on the performance. The values of maximum depth of scour were observed after every one-hour as shown in Table 4. The values of PN for models SQA-5, SQA-6, SQA-15 and SQA-21 are 0.88, 0.65, 0.60, 0.51 respectively. It can be observed that the value of maximum depth of scour after eight hours in the model SQA-15 was 61% of the USBR model SQA-5. The rate of increase of scour in the new model SQA-15 is also less as compared to the USBR model SQA-5.
Discussions
It was observed that a splitter block assists in splitting and spreading of the concentrated jet of water in a wider space in the basin. A wedge shaped block produces more drag in the flow especially by increasing the wake area as compared to other blocks. The stronger vortices are produced in the vertical plane when the expanding jet of water strikes the impact wall. The sheet of water passing through the gap underneath and over the intermediate sill below the impact wall helped in spreading the jet into full width of the basin and lifting the flow. This phenomenon created more horizontal shear and eddies thereby resulting into additional turbulence, friction & formation of sharp discontinuity layers inside the flow. The rounded end sill produces a strong reverse roller at the end of the stilling basin model and high velocity filaments moved away from the bottom of the basin and finally resulted in a reduction in the maximum depth of scour at a farther distance. This condition ultimately leads to sufficient energy dissipation inside the basin and resulted in the increased in the performance.
Conclusions
The performance of stilling basin models can be compared by measuring scour parameters like maximum depth of scour and its location after the end sill, for a constant running time and the same grade of material. A rounded end sill of height equal to the USBR end sills of rectangular and sloping shape is found to perform better. The wedge shaped block is quite effective in spreading the jet and reduction in length of the basin by offering more drag in the flow. The impact wall without notch is better as compared to the impact wall with notch when tested under similar conditions.
The best performing model SQA-15 of length of basin equal to 10.9d (Figure 9) has a wedge shaped splitter block of width equal to 1d placed at 1d from exit of the outlet, a USBR impact wall without notch placed at 4.87d with a gap at bottom equal to 1.66d, an intermediate sill of height 0.5d (slope 1V: 2H) placed below the impact wall and a rounded end sill of height 1.66d. The new stilling basin model SQA-15 also performs much better than the USBR type VI stilling basin model SQA-5 when tested independent of the tailwater. Further the new recommended model SQA-15 (Figure 9) also performing quite well when tested under a longer run time as compared to the USBR type VI model SQA-5. Also, there is a reduction in length of the new basin by more than 15% as compared to USBR type VI model (SQA-5). The use of model SQA-15 would lead to a saving in cost of construction without affecting performance. However, models are to be tested in a range of Froude no for wider applicability.
Table 2 Table 1 Table 3 Table 4 Figures 1-3: Model SQA-1 & SQA-4; Model SQA-2 & SQA-5; Model SQA-3 & SQA-6 Figures 1-3 Figure 7: Shapes of splitter block tested Figure 7 Figures 8-9: Recommended model SQA-21; recommended model SQA-15 Figures 8-9 Figures 4-6: Model SQA-7, SQA-8 and SQA-9 Figures 4-6 Eq 1a Eq 8 Eq 9 Eq 4 Eq 7 Eq 5 Eq 3 Eq 6 Eq 2 Eq 1 Author Info:
Assistant Professor, Civil Engineering Department, National Institute of Technology (Deemed University) Kurukshetra.136119. Haryana. INDIA. Email: drarun_goel @ yahoo.co.in
TablesTable 2 Table 1 Table 3 Table 4