Runner core cavitation near full load in Francis turbines
3 October 2008Experimental evidence has shown that spiral-form cavitating vortex ropes may appear at full load of Francis turbines. The pressure fluctuations arising simultaneously with the spiraling vortices may endanger the turbine. These flow instabilities are explained in this paper based on the theory of rotating stall. By P Krishnamachar, Arpad A Fay and Saroj Rangnekar
It is well known that in Francis turbines pressure oscillations appear in the draft tubes at part-load operation. These oscillations may be so high that below a limit value part-load operation is not allowed. To avoid this limitation, or at least to lessen the limit value, continues to be an essential research target even today. In a few cases harmful instabilities were experienced even at full load. This purpose of this paper is to explain full load instabilities.
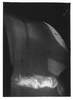
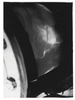
Thoma (1910) and Ackeret (1930) [1] have studied this instability problem of Francis turbines but Deriaz (1960) was the first to give an explanation based on the precession movement of gyroscopes [2]. He also found close correlation between the pressure fluctuations in the draft tube and the rotating cavitation ropes observed downstream of the hub. Straight ropes (Figure 1, Photo 1) cause no or small fluctuations but spiral-form ropes (Figure 2, Photo 2) are dangerous in this respect. In the tests of Deriaz the proportion of the speed of the rotating cavitation spiral to the shaft speed was between 14 to 34%, and this proportion was nearly the same for the prototype as for the model. Later, Giraud (1966) reported that the amplitudes of the fluctuations also show similar variation in the model as in the prototype [3]. Thus it became clear rather early that these flow instabilities of the prototypes may be studied by their model turbines. A number of investigations have been carried out over the years, with recent important papers being [4], [5], and [6], yet it seems that the subject is not settled yet.
Full load instability is still less known. Deriaz [2] expressed an opinion that runner blade cavitation may play an important role in the formation of spiral-form cavitating ropes at full load. Recently Brekke [7] reported power oscillations of 50 to 60MW at full load for a prototype of 315MW. He calculated the interaction of the rope cavity with other water accumulators in the system (surge tank and atmospheric air at draft tube end) and explained full load surges on this basis. This paper states that rotating stall may present a further possible explanation for full load surges.
Model tests
Fay reported model tests of a Francis turbine [8, 9] with nq = nQ0.5H-0.75 = 34 [rpm,m3/sec,m], throat diameter D = 260mm, net head H = 30m, constant during the tests. Development of cavitation with decreasing s is shown in Figure 1, obtained with full opening at n11 = nD/H0.5 = 45.3 [rpm,m,m], near full load point of prospected prototype. With decreasing s a straight cavitation rope (Photo 1) was developed, and no pressure fluctuations were observed under such flow conditions.
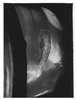
Figure 2 shows the development of the cavitation at full opening, as in Figure 1, but at smaller unit speed: n11 = 41 (Point B in Figure 3). With gradually decreasing s a spiral-form cavitating rope (Photo 2) was found. At smaller s values it was transformed into multiple cavitation ropes (Photo 3), and later into large cavities (Figure 2).
It is not the cavitation that generates pressure fluctuations. The fluctuations are also present in the model at high s values when cavitation is suppressed. The fluctuations are caused by the spiraling flow that results in a rotating pressure field. Solid spirals without core cavity (at maximum s in Figure 2) may be more dangerous than the flows with single cavitating ropes (at smaller s values). The cavitation only renders the vortex lines visible. Multiple ropes are less dangerous, and large cavities are not dangerous.
Power surges are due to the fact that the spiraling flow enters into the bent draft tube. The elbow draft tube drifts the spiral in the direction of the tailrace and renders it eccentric with the runner. The spiral and hence the pressure field are no longer coaxial with the runner. At inlet of the bend, during half rotation of the spiral, the low pressure zone (the core of the spiral) moves from the headwater side to the tailwater side of the draft tube, and so the flow resistance of the draft tube changes in phase with the rope rotation. According to this concept, the power fluctuations are caused by changes in the draft tube resistance.
In straight draft tubes, like in old Francis designs, the spiraling flows may be present, but the flow leaves the draft tube smoothly meaning no power fluctuations are generated.
Figure 2 also helps explain the effect of air entrainment. When air enters at the hub of the turbine, then the pressure increases in the rope. The pressure differential between the main flow and the rope becomes smaller. The flow conditions are identical with those measured at smaller s values. As seen from Figure 2 decreasing s (or increasing air entrainment) results in thick, rotation-symmetric ropes, and these do not generate fluctuations in the bend. This is one of the reasons why air entrainment helps reduce power pulsations. It is also seen from Figure 2 that air entrainment may be effective to suppress spiraling flow without an essential change in efficiency.
Figure 3 shows the position of the above operating points in the model diagram. Point A refers to Figure 1 with straight rope, and Point B to Figure 2 with spiral rope.
The safe operating region with straight vortex filament or no vortex filament lies in between the two zones of the spiraling flows (Figure 3). It is worth noting that this regime of turbine operation is largely free from stall. Prototype operating points must be placed into this safe strip.
If maximum prototype power point (upper left corner of prototype region) happens to be in the range of spiraling flows, then pressure surges appear. This may be the reason why power fluctuations were obtained in some prototypes at full load.
Rotating stall
Rotating stall is a well-known phenomenon in compressors and blowers [10, 16, 17]. It may also appear in incompressible flows, such as in radial vaneless diffusers [11], and in pump impellers [12]. There is no reason why rotating stall should not appear in hydraulic turbines near blade stalling conditions.
Stall has been clearly defined for flows around single airfoils (Figure 4). If the attack angle of the airfoil is near the ideal incidence angle of the airfoil, then a smooth flow leaves the airfoil and considerable lift coefficient may be generated (for narrow airfoils this range is about ±10 degree). If the attack angle largely departs from the ideal angle then a highly turbulent separated flow leaves the airfoil and the lift coefficient breaks down (Figure 4). The latter condition is called the stall. It may appear either on the suction or on the pressure side of the airfoil.
Stall may also appear in Francis runners (Figure 5) on the suction side or on the pressure side of the runner blade depending upon the angle of attack being very much more or less than the optimum. Stall may occur in the runner either at crown or at band or in between depending on runner geometry.
The basic concept of rotating stall is explained in the theory of compressors [16, 17]. If the runner blades are not exactly similar, then with increasing or decreasing attack angle one of the blades begins stalling. The flow in the stalling channel affects the flow in the neighbouring flow channels. However, since the neighbouring channels are on the verge of stalling, a small pull from one side may trigger stalling in one of the neighbouring channels. When the neighbouring channel experiences stall, then the stall disappears in the original channel. Thus, the stall moves from blade to blade, rotating in the runner.
At the downstream end of the stalling channel, the pressure is certainly lower than at the other channels. The low-pressure zone downstream of the stalling channel shifts the vortex core (or rope) from the centerline towards the draft tube wall. Thus, the moving stall generates a spiraling vortex filament rotating together with the stalling region.
The theory of rotating stall is complicated. There are multiple stalls when more than one stall rotates simultaneously. However, the beginning of the stall (the transition from smooth flow to stall) usually involves a single stall in one channel only, and the rotation of the single stall generates a single spiral in the flow. Further development of the stall with changing attack angle may involve more stalling channels, multiple rotating stalls, multiple vortex lines and multiple cavitating ropes.
The above theory for the pressure pulsations in Francis turbines also explains why Kaplan turbines are less susceptible to such pulsations. In Kaplan turbines, operating on the cam curve, the runner blades are always turned to match with the inlet velocities, and so stall is avoided in the normal operating range.
Based on this last point, it should be noted that propeller turbines with single regulation of the guide vanes may have similar instability problems with rotating field of pressure fluctuations as Francis turbines, but perhaps to a lesser intensity as they operate under lower pressures or heads.
In the studies on spiraling flows in Francis turbines [2, 13, 14, 15] the speed of the spiral was about 14% to 53% of the runner speed. In compressors the speed of the rotating stall is similarly at a fraction of the rotor speed [16, 17], below about 50%. This seems to indicate some similarity between these flows where stall initiated vortex ropes are concerned.
Thus the main points that support the postulation of rotating stall in Francis runners are:
• Flow separation in blowers and pumps begins with rotating stall; why would Francis runners be exceptions?
• Calculated attack angles of the vanes at the operating points of the limiting lines of spiraling flows (Figure 3) are such that stall is likely. Exactness of the statement is dependent on the criterion of stall.
• Occurrence of pressure fluctuations at full load agrees with the above concepts.
• Turbines operating with straight draft tubes do not suffer from power fluctuations. This indicates the role of the draft tube bend.
• Effect of air entrainment also explains the stall connection: with increasing air flow-rate the diameter of the air-vapor rope is increasing, with multiple rotating stall and non-spiraling flow the result.
• Kaplan turbines, with runner blades adjusted to a favorable position to avoid stall, are less susceptible to such pressure fluctuations.
• The fact that the rotation of the spiral lags when compared to the rotation of the blades indicates that the cause of the spiral moves from blade to blade, like rotating stall.
Conclusions
Residual rotation, to which runner core cavitation is attributed, results in a general whirl in the flow after a fixed bladed runner, a vortex coaxial with the turbine with the core attached to the runner cone. There is no reason for its development into a spiral attached to the blades and being eccentric with the runner. Thus rotating stall has greater, if not exclusive, claim to spiral cores.
Full load fluctuations are also due to spiraling flows, for which rotating stall offers an explanation, correlating with the experimental findings.
The properties of rotating stall are not well known. However, understanding the physical background of the instabilities may help model turbine designers to develop geometries of wide safe operating range. Prototype designers and operators should be cautious and place the prototype operating points into the safe strip. Otherwise there is no other remedy for the instability than air entrainment.
The authors are: P Krishnamachar, Consultant, 151 Riverwood Avenue, Bedminster, NJ 07921, USA
Arpad A Fay, Consultant, To u 16, Vertessomlo, 2823 Hungary
Saroj Rangnekar, Professor and Head of Energy Centre, M. A. National Institute of Technology, Bhopal, India